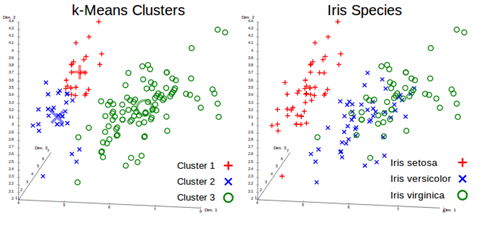
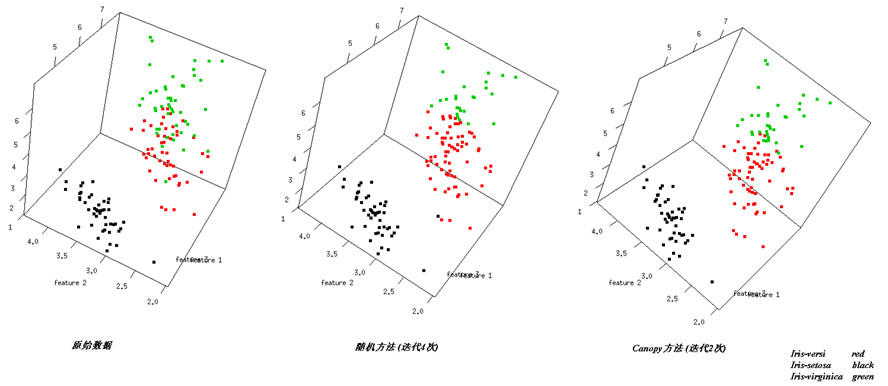
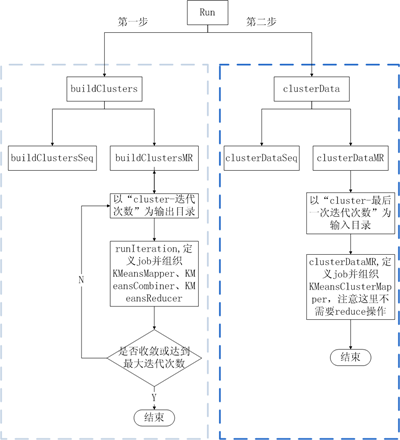
这几天在看hadoop相关的书籍,看到很多书里面提到mahout这个库,感觉非常强大,就在网上找了一些相关的文章转过来。
转自:http://www.cnblogs.com/vivounicorn/archive/2011/09/23/2186483.html
———————正文开始———————-
聚类是机器学习里很重要的一类方法,基本原则是将“性质相似”(这里就有相似的标准问题,比如是基于概率分布模型的相似性又或是基于距离的相似性)的对象尽可能的放在一个Cluster中而不同Cluster中对象尽可能不相似。对聚类算法而言,有三座大山需要爬过去:(1)、a large number of clusters,(2)、a high feature dimensionality,(3)、a large number of data points。在这三种情况下,尤其是三种情况都存在时,聚类的计算代价是非常高的,有时候聚类都无法进行下去,于是出现一种简单而又有效地方法:Canopy Method,说简单是因为它不用什么高深的理论或推导就可以理解,说有效是因为它的实际表现确实可圈可点。
一、基本思想
1、基于Canopy Method的聚类算法将聚类过程分为两个阶段
Stage1、聚类最耗费计算的地方是计算对象相似性的时候,Canopy Method在第一阶段选择简单、计算代价较低的方法计算对象相似性,将相似的对象放在一个子集中,这个子集被叫做Canopy ,通过一系列计算得到若干Canopy,Canopy之间可以是重叠的,但不会存在某个对象不属于任何Canopy的情况,可以把这一阶段看做数据预处理;
Stage2、在各个Canopy 内使用传统的聚类方法(如K-means),不属于同一Canopy 的对象之间不进行相似性计算。
从这个方法起码可以看出两点好处:首先,Canopy 不要太大且Canopy 之间重叠的不要太多的话会大大减少后续需要计算相似性的对象的个数;其次,类似于K-means这样的聚类方法是需要人为指出K的值的,通过Stage1得到的Canopy 个数完全可以作为这个K值,一定程度上减少了选择K的盲目性。
2、聚类精度
对传统聚类来说,例如K-means、Expectation-Maximization、Greedy Agglomerative Clustering,某个对象与Cluster的相似性是该点到Cluster中心的距离,那么聚类精度能够被很好保证的条件是:
对于每个Cluster都存在一个Canopy,它包含所有属于这个Cluster的元素。
如果这种相似性的度量为当前点与某个Cluster中离的最近的点的距离,那么聚类精度能够被很好保证的条件是:
对于每个Cluster都存在若干个Canopy,这些Canopy之间由Cluster中的元素连接(重叠的部分包含Cluster中的元素)。
数据集的Canopy划分完成后,类似于下图:
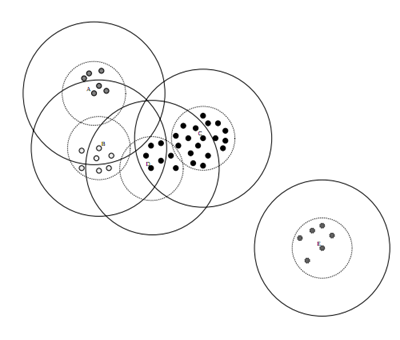
二、单机生成Canopy的算法
(1)、将数据集向量化得到一个list后放入内存,选择两个距离阈值:T1和T2,其中T1 > T2,对应上图,实线圈为T1,虚线圈为T2,T1和T2的值可以用交叉校验来确定;
(2)、从list中任取一点P,用低计算成本方法快速计算点P与所有Canopy之间的距离(如果当前不存在Canopy,则把点P作为一个Canopy),如果点P与某个Canopy距离在T1以内,则将点P加入到这个Canopy;
(3)、如果点P曾经与某个Canopy的距离在T2以内,则需要把点P从list中删除,这一步是认为点P此时与这个Canopy已经够近了,因此它不可以再做其它Canopy的中心了;
(4)、重复步骤2、3,直到list为空结束。
三、并行策略
并行点是比较明显的,就是生成Canopy的过程可以并行,第一阶段,各个slave可以依据存储在本地的数据,各自在本地用上述算法生成若干Canopy,最后在master机器将这些Canopy用相同算法汇总后得到最终的Canopy集合,第二阶段聚类操作就利用最终的Canopy集合进行。
用map-reduce描述就是:datanode在map阶段,利用上述算法在本地生成若干Canopy,之后通过reduce操作得到最终的Canopy集合。
四、Mahout源码安装
正式使用Mahout之前需要做以下准备工作:
1、在http://mahout.apache.org/下载最新的Mahout 0.5源码包;
2、安装mvn,可以在终端输入:sudo apt-get install maven2具体方法可以参照:http://www.mkyong.com/maven/how-to-install-maven-in-ubuntu/;
3、安装Mahout源码,可以参照这里的方法进行:https://cwiki.apache.org/confluence/display/MAHOUT/BuildingMahout;
4、打开eclipse,在“Help”菜单下单击“Install New Software…”,在地址栏添加:http://m2eclipse.sonatype.org/sites/m2e,之后把复选框勾上,然后一路Next即可。
5、最后在eclipse的“File”菜单单击“Import…”,选择“Existing Maven Projects”,Next后选择Mahout源码所在目录,将感兴趣的项目勾上,最后完成步骤即可。mahout-core、mahout-examples和mahout-math是下一步我们需要的。
五、Mahout的Canopy Clustering
mahout实现了一个Canopy Clustering,大致思路与前两节用的方法一样,用了两个map操作和一个reduce操作,首先用一个map和一个reduce生成全局Canopy集合,最后用一个map操作进行聚类。可以在mahout-core下的src/main/java中的package:org.apache.mahout.clustering.canopy中找到相关代码:
1、数据模型
Mahout聚类算法将对象以Vector的方式表示,它同时支持dense vector和sparse vector,一共有三种表示方式(它们拥有共同的基类AbstractVector,里面实现了有关Vector的很多操作):
(1)、DenseVector
位于mahout-math文件夹下的src/main/java中的package:org.apache.mahout.clustering.math中,它实现的时候用一个double数组表示Vector(private double[] values), 对于dense data可以使用它;
(2)、RandomAccessSparseVector
位于mahout-math文件夹下的src/main/java中的package:org.apache.mahout.clustering.math中,它用来表示一个可以随机访问的sparse vector,只存储非零元素,数据的存储采用hash映射:OpenIntDoubleHashMap;
关于OpenIntDoubleHashMap,其key为int类型,value为double类型,解决冲突的方法是double hashing,可能是我获取的源码问题,没有在0.5中找到它的source code,可以从http://grepcode.com/file/repo1.maven.org/maven2/org.apache.mahout/mahout-collections/0.3/org/apache/mahout/math/map/OpenIntDoubleHashMap.java#OpenIntDoubleHashMap.indexOfInsertion%28int%29中查看0.3中代码和较详细注释;
(3)、SequentialAccessSparseVector
位于mahout-math文件夹下的src/main/java中的package:org.apache.mahout.clustering.math中,它用来表示一个顺序访问的sparse vector,同样只存储非零元素,数据的存储采用顺序映射:OrderedIntDoubleMapping;
关于OrderedIntDoubleMapping,其key为int类型,value为double类型,存储的方式让我想起了Libsvm数据表示的形式:非零元素索引:非零元素的值,这里用一个int数组存储indices,用double数组存储非零元素,要想读写某个元素,需要在indices中查找offset,由于indices应该是有序的,所以查找操作用的是二分法。
2、如何抽象Canopy?
可以从Canopy.java文件及其父类中找到答案,Mahout在实现时候还是很巧妙的,一个Canopy包含的字段信息主要有:
1)、private int id; #Canopy的id
2)、private long numPoints; #Canopy中包含点的个数,这里的点都是Vector
3)、private Vector center; #Canopy的重心
4)、private Vector Radius; #Canopy的半径,这个半径是各个点的标准差,反映组内个体间的离散程度,它的计算依赖下面要说的s0、s1和s2。
它并不会真的去用一个list去存储其包含的点,因为将来的计算并不关心这些点是什么,而是与由这些点得到的三个值有关,这里用三个变量来表示:
5)、private double s0; #表示Canopy包含点的权重之和,
6)、private Vector s1; #表示各点的加权和,
7)、private Vector s2; #表示各点平方的加权和,
以下是它的核心操作:
8)、public void computeParameters(); #根据s0、s1、s2计算numPoints、center和Radius,其中numPoints=(int)s0,center=s1/s0,Radius=sqrt(s2s0-s1s1)/s0,简单点来,假设所有点权重都是1,那么:
%5e2%7d+%7d%7bn%7d%7d) ,其中
,其中
+%7d%7bn%7d%7d%0a%0a)

 ,其中
,其中

9)、public void observe(VectorWritable x, double weight); #每当有一个新的点加入当前Canopy时都需要更新s0、s1、s2的值,这个比较简单。
3、Canopy Clustering的Map-Reduce实现
Canopy Clustering的实现包含单机版和MR两个版本,单机版就不多说了,MR版用了两个map操作和一个reduce操作,当然是通过两个不同的job实现的,map和reduce阶段执行顺序是:CanopyMapper –> CanopyReducer –> ClusterMapper,我想对照下面这幅图来理解:
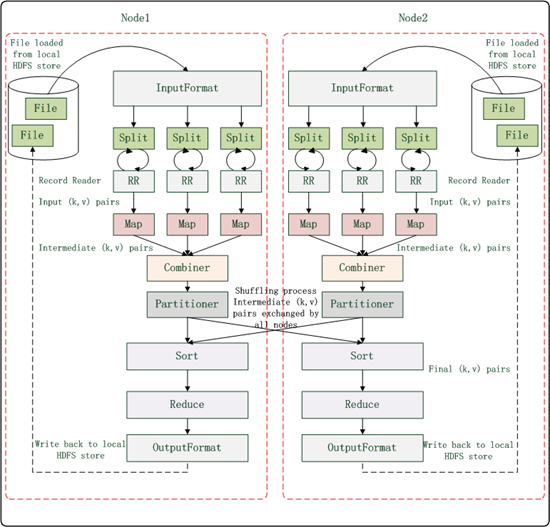
(1)、首先是InputFormat,这是从HDFS读取文件后第一个要考虑的问题,mahout中提供了三种方式,都继承于FileInputFormat<K,V>:
|
**Format**
|
**Description**
|
**Key**
|
**Value**
|
|
TextInputFormat
|
Default format; reads lines of text files (默认格式,按行读取文件且不进行解析操作,基于行的文件比较有效)
|
The byte offset of the line(行的字节偏移量) |
The line contents (整个行的内容) |
|
KeyValueInputFormat
|
Parses lines into key, val pairs (同样是按照行读取,但会搜寻第一个tab字符,把行拆分为(Key,Value) pair)
|
Everything up to the first tab character(第一个tab字符前的所有字符)
|
The remainder of the line (该行剩下的内容)
|
|
SequenceFileInputFormat
|
A Hadoop-specific high-performance binary format (Hadoop定义的高性能二进制格式)
|
user-defined (用户自定义)
|
user-defined (用户自定义)
|
在这里,由于使用了很多自定义的类型,如:表示vector的VectorWritable类型,表示canopy的canopy类型,且需要进行高效的数据处理,所以输入输出文件选择SequenceFileInputFormat格式。由job对象的setInputFormatClass方法来设置,如:job.setInputFormatClass(SequenceFileInputFormat.class),一般在执行聚类算法前需要调用一个job专门处理原始文件为合适的格式,比如用InputDriver,这点后面再说。
(2)、Split
一个Split块为一个map任务提供输入数据,它是InputSplit类型的,默认情况下hadoop会把文件以64MB为基数拆分为若干Block,这些Block分散在各个节点上,于是一个文件就可以被多个map并行的处理,也就是说InputSplit定义了文件是被如何切分的。
(3)、RR
RecordReader类把由Split传来的数据加载后转换为适合mapper读取的(Key,Value) pair,RecordReader实例是由InputFormat决定,RR被反复调用直到Split数据处理完,RR被调用后接着就会调用Mapper的map()方法。
“RecordReader实例是由InputFormat决定”这句话怎么理解呢?比如,在Canopy Clustering中,使用的是SequenceFileInputFormat,它会提供一个 SequenceFileRecordReader类型,利用SequenceFile.Reader将Key和Value读取出来,这里Key和Value的类型对应Mapper的map函数的Key和Value的类型,Sequence File的存储根据不同压缩策略分为:NONE:不压缩、RECORD:仅压缩每一个record中的value值、BLOCK:将一个block中的所有records压缩在一起,有以下存储格式:
**Uncompressed SequenceFile
**Header
Record
Record length
Key length
Key
Value
A sync-marker every few 100 bytes or so.
**Record-Compressed SequenceFile
**Header
Record
Record length
Key length
Key
Compressed Value
A sync-marker every few 100 bytes or so.
Block-Compressed SequenceFile Format
Header
Record Block
Compressed key-lengths block-size
Compressed key-lengths block
Compressed keys block-size
Compressed keys block
Compressed value-lengths block-size
Compressed value-lengths block
Compressed values block-size
Compressed values block
A sync-marker every few 100 bytes or so.
具体可参见:http://www.189works.com/article-18673-1.html
(4)、CanopyMapper
CanopyMapper类里面定义了一个Canopy集合,用来存储通过map操作得到的本地Canopy。
setup方法在map操作执行前进行必要的初始化工作;
它的map操作很直白,就是将传来的(Key,Value) pair(以后就叫“点”吧,少写几个字)按照某种策略加入到某个Canopy中,这个策略在CanopyClusterer类里说明;
在map操作执行完后,调用cleanup操作,将中间结果写入上下文,注意这里的Key是一个固定的字符串“centroid”,将来reduce操作接收到的数据就只有这个Key,写入的value是所有Canopy的中心点(是个Vector哦)。
(5)、Combiner
可以看做是一个local的reduce操作,接受前面map的结果,处理完后发出结果,可以使用reduce类或者自己定义新类,这里的汇总操作有时候是很有意义的,因为它们都是在本地执行,最后发送出得数据量比直接发出map结果的要小,减少网络带宽的占用,对将来shuffle操作也有益。在Canopy Clustering中不需要这个操作。
(6)、Partitioner & Shuffle
当有多个reducer的时候,partitioner决定由mapper或combiner传来的(Key,Value) Pair会被发送给哪个reducer,接着Shuffle操作会把所有从相同或不同mapper或combiner传来的(Key,Value) Pair按照Key进行分组,相同Key值的点会被放在同一个reducer中,我觉得如何提高Shuffle的效率是hadoop可以改进的地方。在Canopy Clustering中,因为map后的数据只有一个Key值,也就没必要有多个reducer了,也就不用partition了。关于Partitioner可以参考:http://blog.oddfoo.net/2011/04/17/mapreduce-partition分析-2/
(7)、CanopyReducer
CanopyReducer 类里面同样定义了一个Canopy集合,用来存储全局Canopy。
setup方法在reduce操作执行前进行必要的初始化工作,这里与mapper不同的地方是可以对阈值T1、T2(T1>T2)重新设置(这里用T3、T4表示),也就是说map阶段的阈值可以与reduce阶段的不同;
reduce操作用于map操作一样的策略将局部Canopy的中心点做重新划分,最后更新各个全局Canopy的numPoints、center、radius的信息,将(Canopy标示符,Canopy对象) Pair写入上下文中。
(8)、OutputFormat
它与InputFormat类似,Hadoop会利用OutputFormat的实例把文件写在本地磁盘或HDFS上,它们都是继承自FileOutputFormat类。各个reducer会把结果写在HDFS某个目录下的单独的文件内,命名规则是part-r-xxxxx,这个是依据hadoop自动命名的,此外还会在同一目录下生成一个_SUCCESS文件,输出文件夹用FileOutputFormat.setOutputPath() 设置。
到此为止构建Canopy的job结束。即CanopyMapper –> CanopyReducer 阶段结束。
(9)、ClusterMapper
最后聚类阶段比较简单,只有一个map操作,以上一阶段输出的Sequence File为输入,setup方法做一些初始化工作并从上一阶段输出目录读取文件,重建Canopy集合信息并存储在一个Canopy集合中,map操作就调用CanopyClusterer的emitPointToClosestCanopy方法实现聚类,将最终结果输出到一个Sequence File中。
(10)、CanopyClusterer
这个类是实现Canopy算法的核心,其中:
1)、addPointToCanopies方法用来决定当前点应该加入到哪个Canopy中,在CanopyMapper和CanopyReducer 中用到,流程如下:
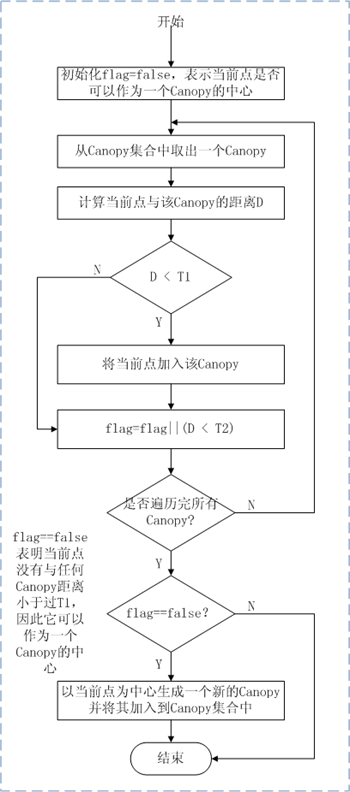
2)、emitPointToClosestCanopy方法查找与当前点距离最近的Canopy,并将(Canopy的标示符,当前点Vector表示)输出,这个方法在聚类阶段ClusterMapper中用到。
3)、createCanopies方法用于单机生成Canopy,算法一样,实现也较简单,就不多说了。
(11)、CanopyDriver
一般都会定义这么一个driver,用来定义和配置job,组织job执行,同时提供单机版和MR版。job执行顺序是:buildClusters –> clusterData。
4、其它
CanopyMapper的输入需要是(WritableComparable<?>, VectorWritable) Pair,因此,一般情况下,需要对数据集进行处理以得到相应的格式,比如,在源码的/mahout-examples目录下的package org.apache.mahout.clustering.syntheticcontrol.canopy中有个Job.java文件提供了对Canopy Clustering的一个版本:
利用InputDriver对数据集进行处理,将(Text, VectorWritable) Pair 以sequence file形式存储,供CanopyDriver使用。InputDriver中的作业配置如下:
5、实例说明
可以用源码生成相关Jar文件,例如:

(1)、准备若干数据集data,要求不同feature之间用空格隔开;
(2)、在master的终端敲入命令:hadoop namenode –format;start-all.sh;用于初始化namenode和启动hadoop;
(3)、在HDFS上建立testdata文件夹,聚类算法会去这个文件夹加载数据集,在终端输入:hadoop dfs –mkdir testdata;
(4)、然后将各个datanode上的数据集data上传到HDFS,在终端输入hadoop dfs –put data testdata/
(5)、进入mahout的那些Jar文件所在路径,在终端敲入:hadoop jar mahout-examples-0.5-job.jar org.apache.mahout.clustering.syntheticcontrol.canopy.Job;
(6)、在localhost:50030查看作业执行情况,例如:
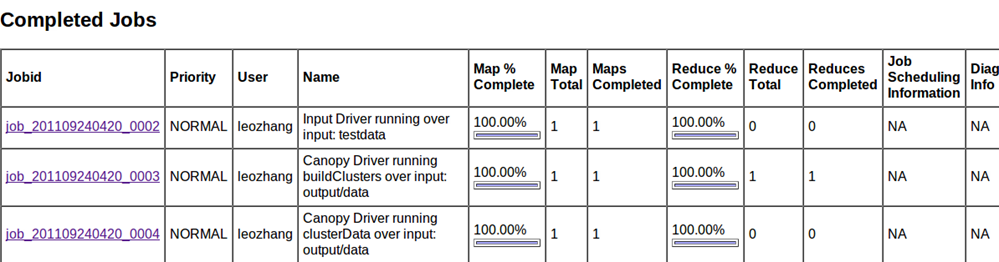
可以看到,第一个作业由InputDriver发起,输入目录是testdata,一共做了一个map操作但没有做reduce操作,第二个作业由CanopyDriver发起,做了一对mapreduce操作,这里对应Canopy生成过程,最后一个作业也由CanopyDriver发起,做了一个map操作,对应Canopy Clustering过程。
(7)、将执行结果抓到本地文件夹,在终端执行:hadoop dfs –get output output,得到目录如下:
 其中聚类结果保存在第一个文件夹中,当然,结果是Sequence File,不能直接双击打开来看。
其中聚类结果保存在第一个文件夹中,当然,结果是Sequence File,不能直接双击打开来看。
6、总结
Mahout中对Canopy Clustering的实现是比较巧妙的,整个聚类过程用2个map操作和1个reduce操作就完成了,Canopy构建的过程可以概括为:遍历给定的点集S,设置两个阈值:T1、T2且T1>T2,选择一个点,用低成本算法计算它与其它Canpoy中心的距离,如果距离小于T1则将该点加入那个Canopy,如果距离小于T2则该点不会成为某个Canopy的中心,重复整个过程,直到S为空。
六、参考资料
1、http://mahout.apache.org/
2、https://cwiki.apache.org/MAHOUT/canopy-clustering.html
3、http://developer.yahoo.com/hadoop/tutorial/
4、http://www.ibm.com/developerworks/cn/web/1103_zhaoct_recommstudy3/
5、http://grepcode.com/file/repo1.maven.org/maven2/org.apache.mahout/mahout-utils/0.5/org/apache/mahout/clustering/conversion/InputDriver.java#InputDriver



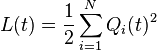
 //这里是前后时间片的这样一个函数的差
//这里是前后时间片的这样一个函数的差![$Q_i(t+1) = max[Q_i(t) + a_i(t) - b_i(t), 0]$](http://upload.wikimedia.org/math/7/d/4/7d477fc326ac80810f13daf6970af2a7.png) //单个队列来看,一个队列下一个时间片积累的数目就是收到的减去处理了的(管你怎么处理,直接扔掉也算是处理了)
//单个队列来看,一个队列下一个时间片积累的数目就是收到的减去处理了的(管你怎么处理,直接扔掉也算是处理了)![$Q_i(t+1)^2 = max[Q_i(t) + a_i(t) - b_i(t), 0]^2 leq (Q_i(t+1) + a_i(t) - b_i(t))^2$](http://upload.wikimedia.org/math/6/c/9/6c983ca5c2585a16ea1a5bbb33d9b5c5.png) //这里为什么就要用平方啊,可耻啊,完全搞不懂想干嘛,而且自己推了一下这个不等式尽然不成立
//这里为什么就要用平方啊,可耻啊,完全搞不懂想干嘛,而且自己推了一下这个不等式尽然不成立 //如果前面的成立,推出这个不等式,里面的B就是界限之类的东西,但是t+1跑哪里去了?被吃了么?
//如果前面的成立,推出这个不等式,里面的B就是界限之类的东西,但是t+1跑哪里去了?被吃了么?![$B(t) = frac{1}{2}sum_{i=1}^N[a_i(t)^2 + b_i(t)^2 - 2a_i(t)b_i(t)]$](http://upload.wikimedia.org/math/8/9/4/8948358643ac90712ab3743646be15ef.png) //上面那个不等式的一部分
//上面那个不等式的一部分![$E[B(t) | Q(t)] leq B$](http://upload.wikimedia.org/math/f/4/5/f450c5db18b8f06a4150c89a6ec934f5.png) //这个期望中间那一竖搞不清楚是要干嘛,但是大致明白是什么意思了,就是B是这个的上限,因为不管怎么样a(t)-b(t)都是个有限数
//这个期望中间那一竖搞不清楚是要干嘛,但是大致明白是什么意思了,就是B是这个的上限,因为不管怎么样a(t)-b(t)都是个有限数![$(Eq. 2) text{ } E[Delta(t) | Q(t)] leq B + sum_{i=1}^N Q_i(t)E[a_i(t) - b_i(t) | Q(t)]$](http://upload.wikimedia.org/math/2/c/e/2ce35121dd5c5dfeebbfe4a2dfdfcc3b.png) //这里就是替换了一下,中间那一竖还是不知道什么意思
//这里就是替换了一下,中间那一竖还是不知道什么意思 :
:![$E[a_i(t) - b_i(t) | Q(t)] leq -epsilon$](http://upload.wikimedia.org/math/2/0/5/2057f70e99546eb61675876580d21155.png) //还是进行一些YY,反正就是先YY个上界(其实不是YY,应该是有道理的,使用了某些技术,比如松弛?)
//还是进行一些YY,反正就是先YY个上界(其实不是YY,应该是有道理的,使用了某些技术,比如松弛?)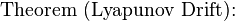
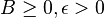 such that for all t and all possible vectors Q(t) the conditional Lyapunov drift satisfies:
such that for all t and all possible vectors Q(t) the conditional Lyapunov drift satisfies:![$E[Delta(t)|Q(t)] leq B - epsilon sum_{i=1}^N Q_i(t)$](http://upload.wikimedia.org/math/e/8/c/e8cb077341bf066f15b5ba286b0baeb6.png) //上面那个公式继续简化,这样就用两个常量限制了这个不等式
//上面那个公式继续简化,这样就用两个常量限制了这个不等式![$frac{1}{t}sum_{tau=0}^{t-1} sum_{i=1}^NE[Q_i(tau)] leq frac{B}{epsilon} + frac{E[L(0)]}{epsilon t}$](http://upload.wikimedia.org/math/8/0/6/80648022337eb4cd3c75ae55001b5ba2.png) //这个公式是下面证明了的,其实就是通过上面一个公式通过一定时间片的累加推出来的一个有意义的结论
//这个公式是下面证明了的,其实就是通过上面一个公式通过一定时间片的累加推出来的一个有意义的结论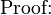
![$E[Delta(t)] leq B - epsilon sum_{i=1}^N E[Q_i(t)]$](http://upload.wikimedia.org/math/4/6/8/4683eaf21caa183a86bd099b307c757d.png) //这就是上上面那个公式,怎么中间的一竖去掉了,忽悠我呢
//这就是上上面那个公式,怎么中间的一竖去掉了,忽悠我呢 and using the law of telescoping sums gives:
and using the law of telescoping sums gives:![$E[L(t)] - E[L(0)] leq Bt - epsilon sum_{tau=0}^{t-1}sum_{i=1}^NE[Q_i(tau)]$](http://upload.wikimedia.org/math/7/f/d/7fd7e2d1ee6ff68bfabf7b5c0c130536.png) //来吧从0加到t+1,然后就搞定了
Using the fact that L(t) is non-negative and rearranging the terms in the above expression proves the result.
//来吧从0加到t+1,然后就搞定了
Using the fact that L(t) is non-negative and rearranging the terms in the above expression proves the result.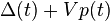

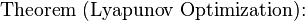
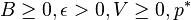 such that for all t and all possible vectors Q(t) the following drift-plus-penalty condition holds:
such that for all t and all possible vectors Q(t) the following drift-plus-penalty condition holds:![$text{ } frac{1}{t}sum_{tau=0}^{t-1} E[p(tau)] leq p^* + frac{B}{V} + frac{E[L(0)]}{Vt}$](http://upload.wikimedia.org/math/5/7/0/57030614bbd29c2db55a9e41a5aa01b9.png)
![$text{ } frac{1}{t}sum_{tau=0}^{t-1} sum_{i=1}^NE[Q_i(tau)] leq frac{B + V(p^* - p_{min})}{epsilon} + frac{E[L(0)]}{epsilon t}$](http://upload.wikimedia.org/math/a/b/1/ab19a60de57b75be61f4b0ee5b1ce694.png)
![$E[Delta(t)] + VE[p(t)] leq B + Vp^* - epsilon sum_{i=1}^NE[Q_i(t)]$](http://upload.wikimedia.org/math/e/d/6/ed6c7d6fe8b066c824c364f81b58a9a4.png)
![$E[L(t)] - E[L(0)] + Vsum_{tau=0}^{t-1}E[p(tau)] leq (B+Vp^*)t - epsilonsum_{tau=0}^{t-1}sum_{i=1}^NE[Q_i(tau)]$](http://upload.wikimedia.org/math/d/d/2/dd2a9932e26bc2f7422255061020e9db.png)
![$- E[L(0)] + Vsum_{tau=0}^{t-1}E[p(tau)] leq (B+Vp^*)t$](http://upload.wikimedia.org/math/f/b/c/fbc26bf6cde74539a3a9615743eac629.png)